In questo articolo vediamo come implementare la moltiplicazione tra matrici utilizzando l’overload dell’operatore * in C#, in modo da mettere a disposizione una sintassi simile a quella disponibile in Matlab.
Cenni matematici
La moltiplicazione tra matrici si chiama anche moltiplicazione riga per colonna perché il risultato della moltiplicazione tra una matrice di dimensioni m x p (dove m è il numero di righe e p il numero di colonne) e una di dimensioni p x n è una matrice di dimensioni m x n dove il valore di ogni cella con coordinate (i, j) è la sommatoria dei prodotti di ciascun elemento sulla riga i della prima matrice con il corrispondente elemento sulla colonna j della seconda. Ecco perché il numero di colonne della prima deve essere uguale al numero di righe della seconda.
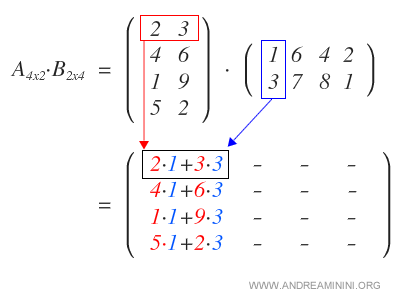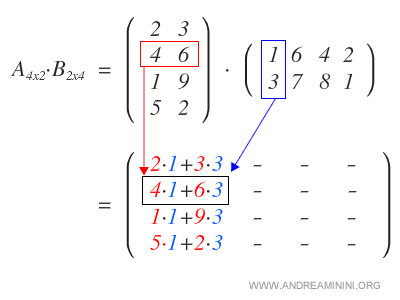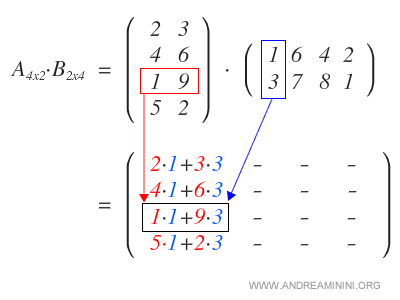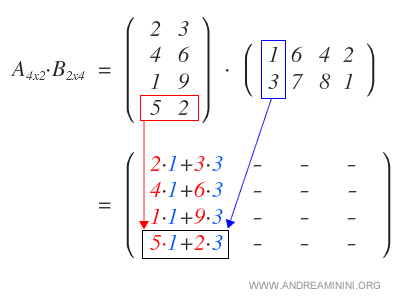
Dalla regola sopra deriva che è possibile moltiplicare un vettore colonna (ovvero una matrice con una o più righe ma una sola colonna) con un vettore riga, ma non viceversa. Vuole anche dire che la moltiplicazione tra matrici non è commutativa.
Implementazione
Seguendo un approccio TDD (Test Driven Development, ovvero prima si definiscono i casi di test, poi si implementa il SUT (System Under Test)), si vuole implementare una classe Matrix che superi i seguenti test (se ne potrebbero in realtà aggiungere altri, ma per semplicità ho selezionato i più interessanti):
[TestClass]
public class MatrixTests : VerifyMSTest.VerifyBase
{
[TestMethod]
[ExpectedException(typeof(ArgumentException))]
public void TestIncompatibleMatricesThrows()
{
var m3 = new Matrix(3, 5) * new Matrix(4, 3);
}
[TestMethod]
public void TestEmptyMatricesGivesEmptyMatrix()
{
var m = new Matrix(0, 0) * new Matrix(0, 0);
Assert.IsTrue(m.Rows == 0 && m.Cols == 0);
}
[TestMethod]
public void TestRowByColumnGives1X1Matrix()
{
var m = new Matrix(1, 3) * new Matrix(3, 1);
Assert.IsTrue(m.Rows == 1 && m.Cols == 1);
}
[DataTestMethod]
[DataRow(true, false)]
[DataRow(false, true)]
[DataRow(true, true)]
[ExpectedException(typeof(ArgumentNullException))]
public void TestNullMatricesThrows(bool firstNull, bool secondNull)
{
var m1 = firstNull ? null : new Matrix(0, 0);
var m2 = secondNull ? null : new Matrix(0, 0);
var m3 = m1 * m2;
}
[TestMethod]
public Task Test2X3By3X2Result()
{
var m1 = new Matrix(2, 3);
var m2 = new Matrix(3, 2);
m1[0, 0] = 1;
m1[0, 1] = 2;
m1[0, 2] = 3;
m1[1, 0] = 11;
m1[1, 1] = 12;
m1[1, 2] = 13;
m2[0, 0] = 1;
m2[0, 1] = 2;
m2[1, 0] = 11;
m2[1, 1] = 12;
m2[2, 0] = 21;
m2[2, 1] = 22;
return Verify(m1 * m2); // Snapshot testing.
}
}L’ultimo metodo di test usa la tecnica dello snapshot testing. Dopo averlo eseguito la prima volta, allo sviluppatore viene presentata una schermata con la serializzazione json dell’oggetto Matrix derivante dalla moltiplicazione. Se ritiene che sia corretto, può approvare lo snapshot in modo che venga usato come riferimento nelle successive esecuzioni del test.
Di seguito il codice della classe Matrix. Oltre all’overloading dell’operatore di moltiplicazione, si noti che viene implementato un indicizzatore per leggere e settare più agevolmente i valori delle singole celle.
public class Matrix
{
/// <summary>
/// Values contained in the matrix. This is a public property for ease of use in snapshot testing. Actually, there are alternatives.
/// </summary>
public float[,] Items { get; }
public int Rows => Items.GetLength(0);
public int Cols => Items.GetLength(1);
/// <summary>
/// Indexer for ease of access to the matrix values.
/// </summary>
public float this[int row, int col] { get => Items[row, col]; set => Items[row, col] = value; }
public Matrix(int rows, int cols) => Items = new float[rows, cols];
/// <summary>
/// Multiplication overloading.
/// </summary>
public static Matrix operator *(Matrix first, Matrix second)
{
ArgumentNullException.ThrowIfNull(first);
ArgumentNullException.ThrowIfNull(second);
if (first.Cols != second.Rows)
throw new ArgumentException("Cannot multiply the given matrices. Wrong dimensions.");
var result = new Matrix(first.Rows, second.Cols);
for (var i = 0; i < result.Rows; i++)
for (var j = 0; j < result.Cols; j++)
for (var k = 0; k < first.Cols; k++)
result[i, j] += first[i, k] * second[k, j];
return result;
}
}